| Sometimes there can be a surprising amount of math where you least expect it - for example, in these paintings; |
| ||
---
Definition of Golden Ratio:
In Mathematics, two quantities are in the Golden Ratio if their Ratio is the same as the Ratio of their sum to the larger of the two quantities.
With two quantities, a and b, a > b > 0, the Golden Ratio, ø = a/b when a/b = (a+b)/a
The Golden Ratio is frequently found in patterns in nature, such as spiral arrangements in shells and plants.
ø is an irrational number with a value of (1+SqRt(5))/2 = 1.6180339887....
Note that a/b = (a+b)/a = a/a + b/a = 1 + b/a In other words ø = 1 + 1/ ø
---
While the Golden Ratio (see Wikipedia) itself is often mentioned in art (e.g. Leonardo Da Vinci used it to compose his paintings), architecture (the Greeks used it to design their buildings), and nature (mathematical basis for naturally occurring patterns), less well-known is the fact ø has some fascinating mathematical properties.
For example starting with ø = 1+ 1/ø (see above), we can derive:
- (Multiply both sides by ø) ø^2 = ø + 1
- (Multiply both sides again by ø) ø^3 = ø^2 + ø
....., 1/(ø^2), 1/ø, 1, ø, ø^2, ø^3, .....
also happens to be a Fibonacci Series, in which the sum of any two consecutive terms generates the next term.
A property that then emerges from this Geometric Fibonacci series is that sums of many different terms in the series can equal the sums of many other terms in the series. E.g.:
ø + ø^2 + ø^3 = 2ø^3 = 1/ø + 3ø^2 = 2ø + 2ø^2 =2 + 4ø etc.
The Swiss architect Le Corbusier, in a quest to design easily-reconfigurable modular buildings, realized that a set of ø-series based modules, i.e. modules whose dimensions were members of the ø series, might allow for building designs with large numbers of permutations and combinations for any given fixed space and fixed set of modules. While Le Corbusier did not succeed in actually creating such modular buildings, his research did bear one fruit: these paintings J.
These paintings incorporate, in their backgrounds, tiling patterns created using ‘tiles’ whose dimensions are based on two INTERLACED ø-series, one series of which is formed by taking the arithmetic mean of consecutive terms of the other series. That is, the elements of one series lie halfway between the elements of the other series, which increases the number of possible ways in which the elements may be combined to add up to other combinations of elements.
All the paintings have the exact same 14 tiles in the background. Every edge of every tile relates to other tile edges in the painting by multiples of golden ratios.
If the Golden Ratio is truly a natural number wired into nature, these tiling patterns should feel naturally aesthetic.
The juxtaposition of a whimsical, illogical form on top of the logical mathematical pattern hopefully creates an anachronism that draws the viewer in to look at the image again and again.



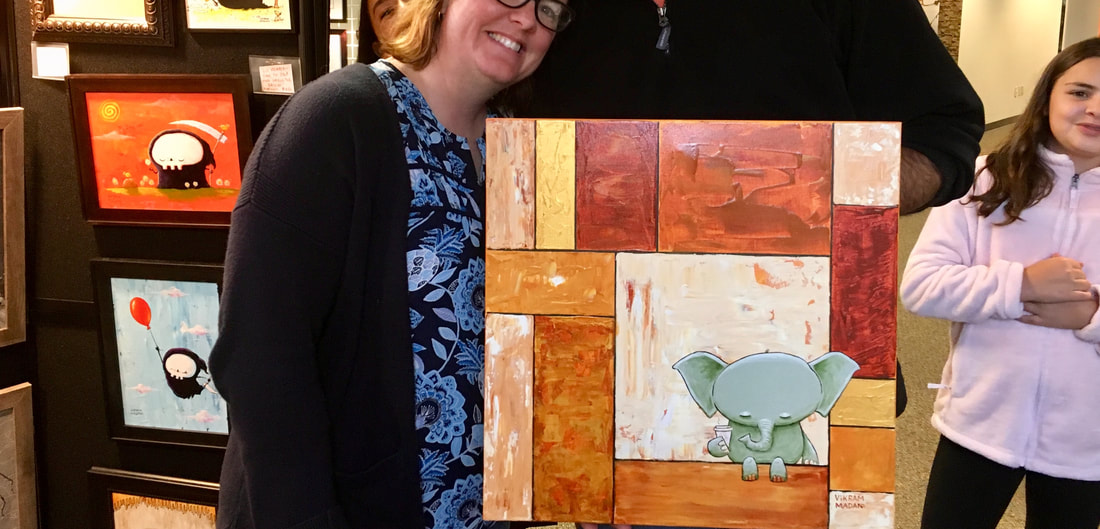

 RSS Feed
RSS Feed